本文代码的实现严重依赖前面的两篇文章:
图像在获取或传输过程中会因各种噪声的干扰使质量下降,这将对后续图像的处理产生不利影响.所以必须对图像进行去噪处理,而去噪所要达到的目的就是在较好去除噪声的基础上,良好的保持图像的边缘等重要细节.在图像去噪领域得到广泛的应用.本博文根据小波的分解与重构原理,实现了基于硬阈值和软阈值函数的小波阈值去噪的C++版本,最终结果与matlab库函数运算结果完全一致。
注本文的大部分文字提取于参考论文
一,小波阈值去噪基本理论
小波阈值处理
小波阈值收缩法是Donoho和Johnstone提出的,其主要理论依据是,小波变换具有很强的去数据相关性,它能够使信号的能量在小波域集中在一些大的小波系数中;而噪声的能量却分布于整个小波域内.因此,经小波分解后,信号的小波系数幅值要大于噪声的系数幅值.可以认为,幅值比较大的小波系数一般以信号为主,而幅值比较小的系数在很大程度上是噪声.于是,采用阈值的办法可以把信号系数保留,而使大部分噪声系数减小至零.小波阈值收缩法去噪的具体处理过程为:将含噪信号在各尺度上进行小波分解,设定一个阈值,幅值低于该阈值的小波系数置为0,高于该阈值的小波系数或者完全保留,或者做相应的“收缩(shrinkage)”处理.最后将处理后获得的小波系数用逆小波变换进行重构,得到去噪后的图像.
阈值函数的选取
阈值去噪中,阈值函数体现了对超过和低于阈值的小波系数不同处理策略,是阈值去噪中关键的一步。设w表示小波系数,T为给定阈值,sign(*)为符号函数,常见的阈值函数有:
硬阈值函数: (小波系数的绝对值低于阈值的置零,高于的保留不变)
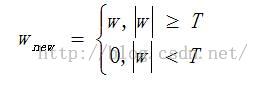
软阈值函数:
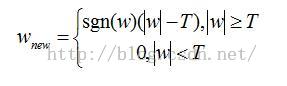
值得注意的是:
1) 硬阈值函数在阈值点是不连续的,在下图中已经用黑线标出。不连续会带来振铃,伪吉布斯效应等。
2) 软阈值函数,原系数和分解得到的小波系数总存在着恒定的偏差,这将影响重构的精度使得重构图像的边缘模糊等现象.
同时这两种函数不能表达出分解后系数的能量分布。见下图:
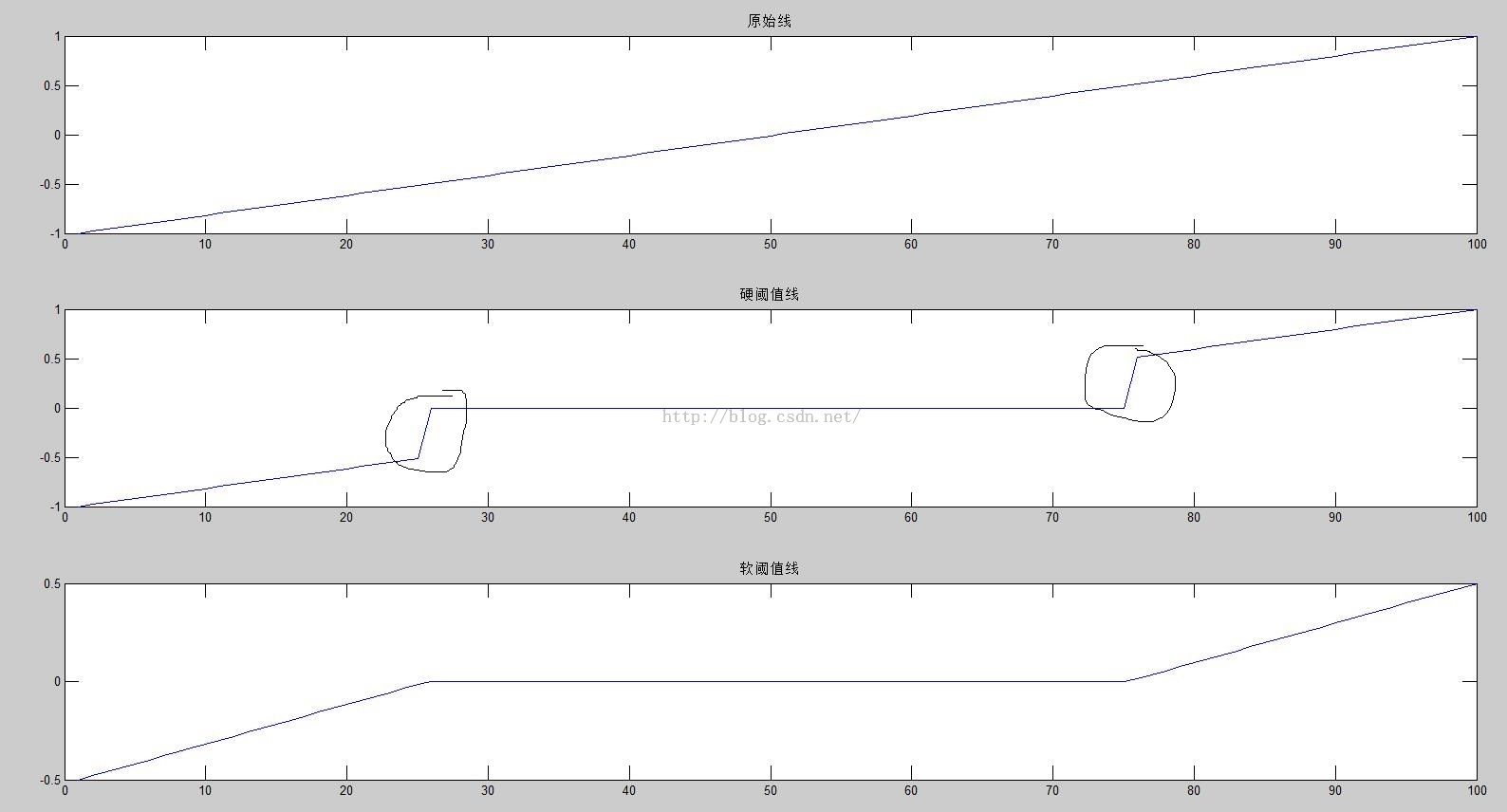
图1
于是不少文章出现了折衷方案,一种新的阈值函数(非本文重点):
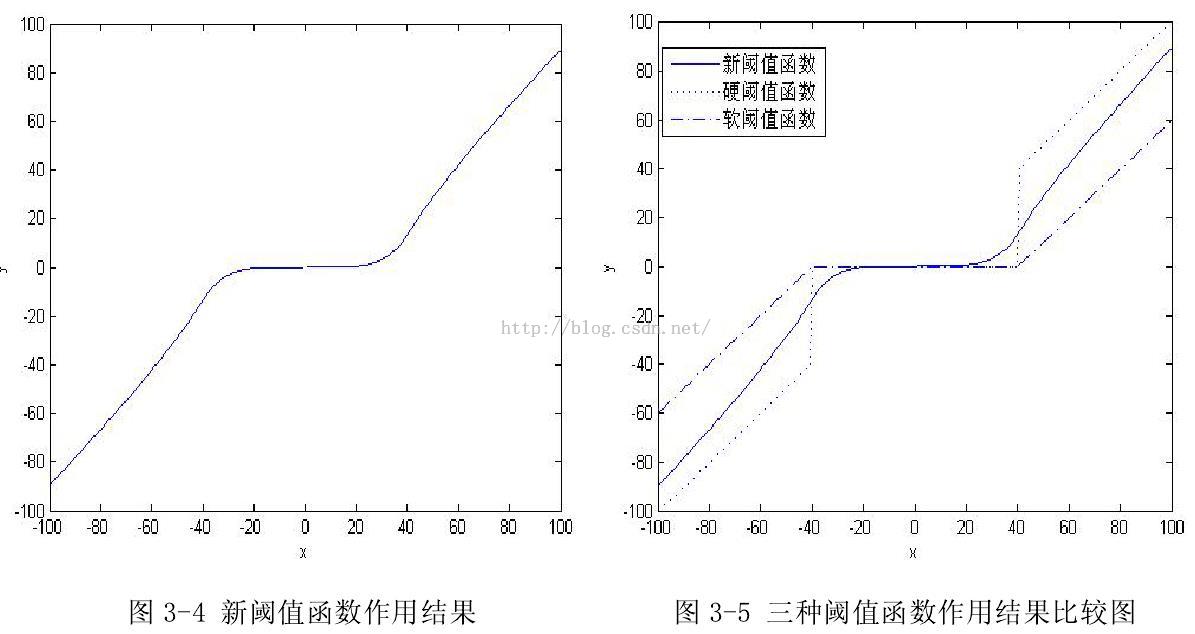
参考代码:
%Generate signal and set threshold.
y = linspace(-1,1,100);
subplot(311);
plot(y);title("原始线");
thr = 0.5;
% Perform hard thresholding.
ythard = wthresh(y,"h",thr);
subplot(312);
plot(ythard);title("硬阈值线");
% Perform soft thresholding.
ytsoft = wthresh(y,"s",thr);
subplot(313);
plot(ytsoft);title("软阈值线");
阈值的确定
选取的阈值最好刚好大于噪声的最大水平,可以证明的是噪声的最大限度以非常高的概率低于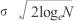
(此阈值是Donoho提出的),其中根号右边的这个参数(叫做sigma)就是估计出来的噪声标准偏差(第一级分解出的小波细节系数,即整个HH系数的绝对值的中值),本文将用此阈值去处理各尺度上的细节系数。
阈值策略
曾经做的ppt挪用过来的。
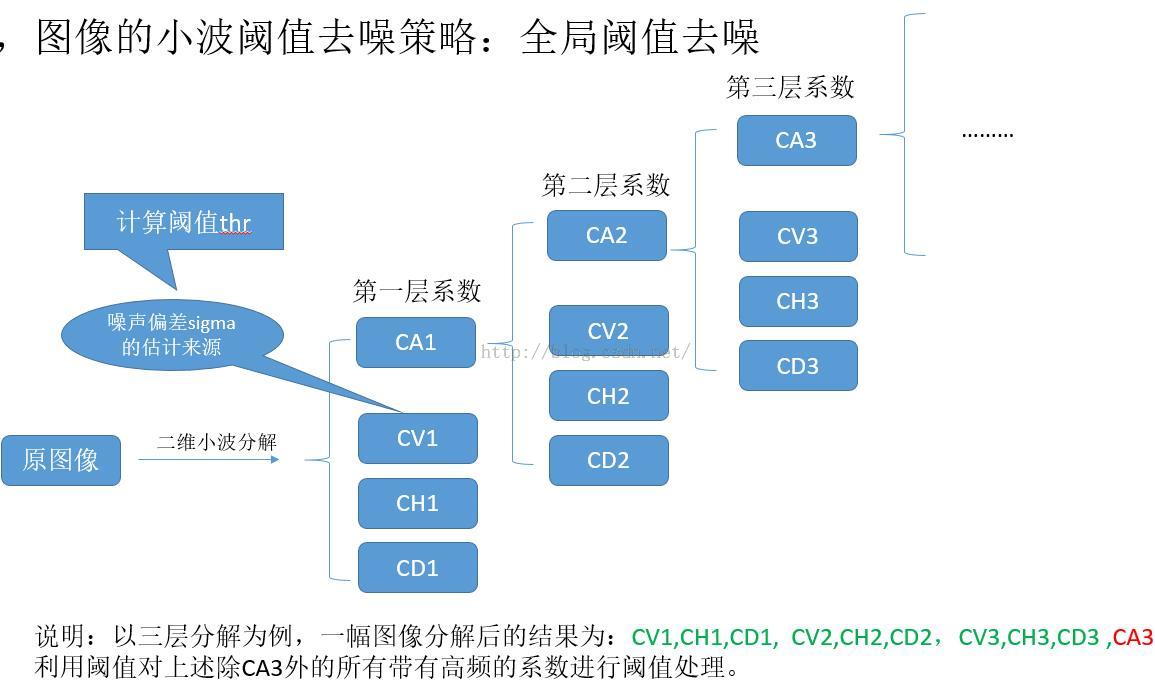
二维信号分解与重构
小波的分解
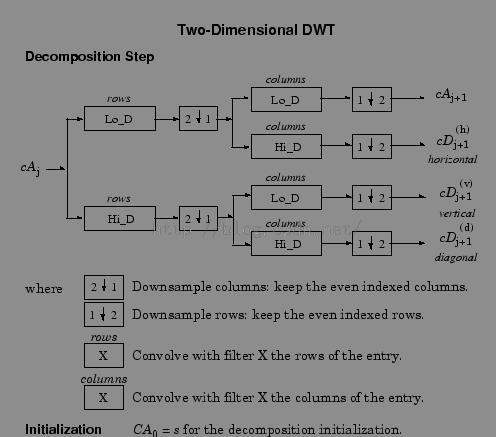
小波的重构
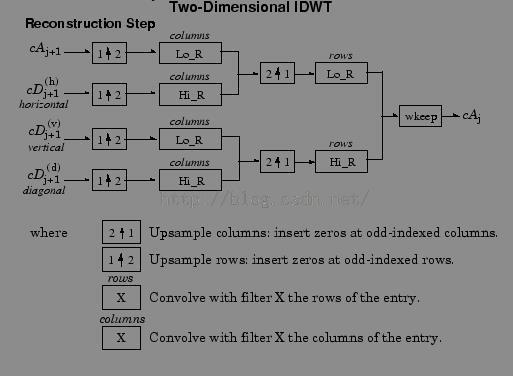
二,Matlab库函数实现
1,核心库函数说明
1)wavedec2
图像的多级小波分解,将返回分解出来的小波系数以及小波系数的各级长度
2)waverec2
多级小波系数的重构,重构出原信号
3)wthresh函数
对系数进行指定类型(全局阈值或者分层阈值)的阈值去噪处理
更具体的函数说明可以在,matlab里键入“doc 函数名”将得到很详细的说明,当然也可以百度
2,软,硬阈值处理效果:



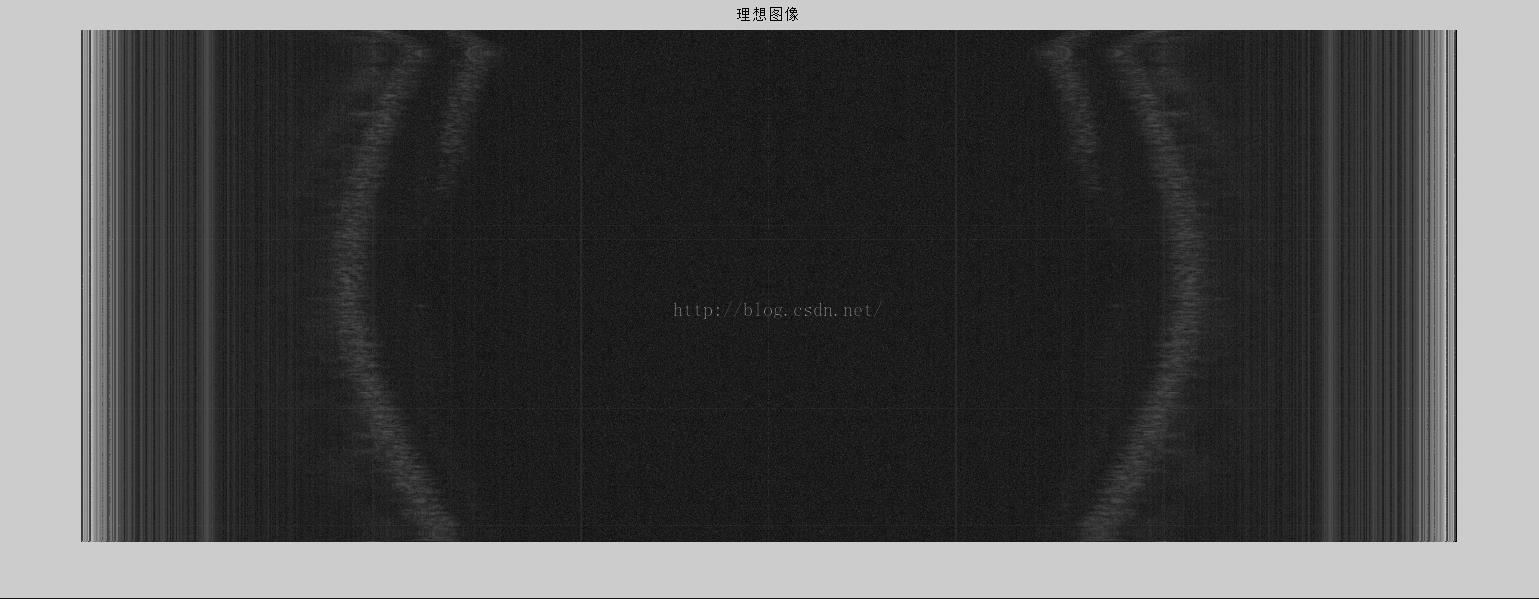
局部放大图像:
四幅图象均放大两倍,便于查看区别



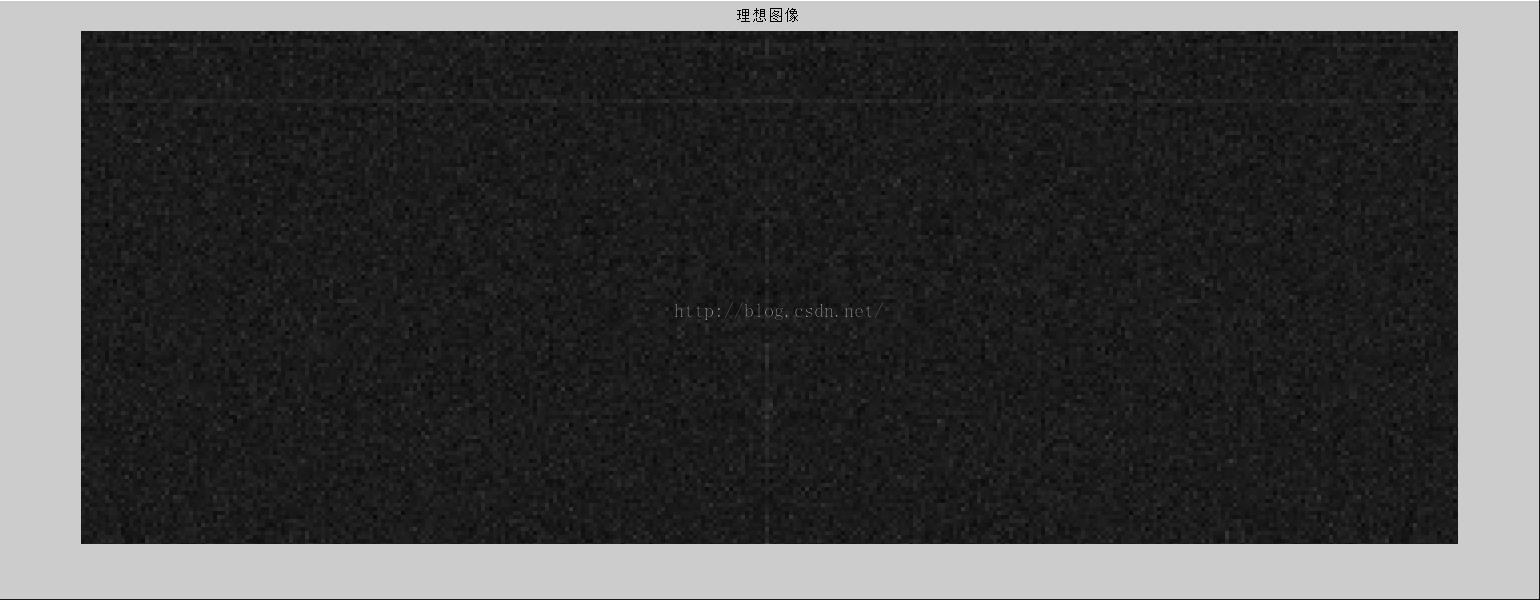
3,完整的代码实现
说明:代码实现对图像一层分解后的细节系数进行全局阈值处理(即LHL,LH,HH均用同一阈值处理),并且阈值是自定义的。
clc;
clear all;
close all;
%%%%%%%%%%%%%%%%%%%%%%%%通过matlab的函数来实现阈值去噪%%%%%%%%%%%%%%%%%%%%%%%%%% %
X=imread("sample1.bmp");%有噪声的图像
X=double(X);
figure(1);
imshow(X,[]);title("原始图像"); %注意,原始图像带有噪声
% 获取输入参数
w = "db3";%小波类型
n = 1;%分解层数
thr = 23.91;%自定义阈值
sorh1 = "h";%硬阈值
sorh2 = "s";%软阈值
% 对图像进行小波分解
[c,l] = wavedec2(X,n,w);
% 对小波系数全局阈值处理
cxch = c;% 保留近似系数
cxcs = c;% 保留近似系数
justdet = prod(l(1,:))+1:length(c);%截取细节系数(不处理近似系数)
% 阈值处理细节系数
cxch(justdet) = wthresh(cxch(justdet),sorh1,thr);%硬阈值去噪
cxcs(justdet) = wthresh(cxcs(justdet),sorh2,thr);%软阈值去噪
%小波重建
xch = waverec2(cxch,l,w);
xcs = waverec2(cxcs,l,w);
figure(2);
imshow(uint8(xch));title("硬阈值去噪图像");
figure(3);
imshow(uint8(xcs));title("软阈值去噪图像");
三,C加加实现
说明:如同一维的阈值去噪一样,在执行自己编写的wavedec2函数时必须先初始化,初始化的目的是为了获取信号的长度,选择的是什么小波,以及分解的等级等信息,然后计算出未来的各种信息,比如每个等级的系数的size,其中共有变量m_msgCL2D记录了这些信息。二维小波分解的初始化函数如下:
//初始化二维图像的分解信息,保存未来需要的信息
bool CWavelet::InitDecInfo2D(
const int height,//预分解的图像的高度
const int width,//预分解的图像的宽度
const int Scale,//分解尺度
const int dbn//db滤波器编号,有默认值
)
{
if (dbn != 3)
SetFilter(dbn);
if (height < m_dbFilter.filterLen - 1 || width < m_dbFilter.filterLen - 1)
{
cerr << "错误信息:滤波器长度大于信号的高度或者宽度!" << endl;
return false;
}
int srcHeight = height;
int srcWidth = width;
m_msgCL2D.dbn = dbn;
m_msgCL2D.Scale = Scale;
m_msgCL2D.msgHeight.resize(Scale + 2);
m_msgCL2D.msgWidth.resize(Scale + 2);
//源图像的尺寸
m_msgCL2D.msgHeight[0] = height;
m_msgCL2D.msgWidth[0] = width;
//每一尺度上的尺寸
for (int i = 1; i <= Scale; i++)//注意:每个尺度的四个分量的长宽是一样的
{
int exHeight = (srcHeight + m_dbFilter.filterLen - 1) / 2;//对称拓延后系数的长度的一半
srcHeight = exHeight;
m_msgCL2D.msgHeight[i] = srcHeight;
int exWidth = (srcWidth + m_dbFilter.filterLen - 1) / 2;//对称拓延后系数的长度一半
srcWidth = exWidth;
m_msgCL2D.msgWidth[i] = srcWidth;
}
m_msgCL2D.msgHeight[Scale + 1] = srcHeight;
m_msgCL2D.msgWidth[Scale + 1] = srcWidth;
//计算总的数据个数
int tmpAllSize = 0;
int curPartSize = 0;
int prePartSize = 0;
for (int i = 1; i <= Scale; i++)
{
curPartSize = m_msgCL2D.msgHeight[i] * m_msgCL2D.msgWidth[i];
tmpAllSize += curPartSize * 4 - prePartSize;
prePartSize = curPartSize;
}
m_msgCL2D.allSize = tmpAllSize;
m_bInitFlag2D = true;
return true;
}
2,核心函数的实现
1)二维信号的单次分解
说明:本函数建立在一维的小波分解函数基础上(DWT)
// 二维数据的小波分解
void CWavelet::DWT2(
double *pSrcImage,//源图像数据(存储成一维数据,行优先存储)
int height,//图像的高
int width,//图像的宽
double *pDstCeof//分解出来的图像系数
)
{
if (!m_bInitFlag2D)
{
cerr << "错误信息:未初始化,无法对信号进行分解!" << endl;
return;
}
if (pSrcImage == NULL || pDstCeof == NULL)
{
cerr << "错误信息:dwt2数据无内存" << endl;
Sleep(3000);
exit(1);
}
int exwidth = (width + m_dbFilter.filterLen - 1) / 2 * 2;//pImagCeof的宽度
int exheight = (height + m_dbFilter.filterLen - 1) / 2 * 2;//pImagCeof的高度
double *tempImage = new double[exwidth*height];
// 对每一行进行行变换
double *tempAhang = new double[width];
double *tempExhang = new double[exwidth]; // 临时存放每一行的处理数据
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
tempAhang[j] = pSrcImage[i*width + j];//提取每一行的数据
DWT(tempAhang, width, tempExhang);
for (int j = 0; j < exwidth; j++)
tempImage[i*exwidth + j] = tempExhang[j];
}
// 对每一列进行列变换
double *tempAlie = new double[height]; // 临时存放每一列的转置数据
double *tempexlie = new double[exheight]; // 临时存放每一列的处理数据
for (int i = 0; i < exwidth; i++)
{
// 列转置
for (int j = 0; j < height; j++)
tempAlie[j] = tempImage[j*exwidth + i];//提取每一列数据
//执行变换
DWT(tempAlie, height, tempexlie);
// 反转置
for (int j = 0; j < exheight; j++)
pDstCeof[j*exwidth + i] = tempexlie[j];
}
AdjustData(pDstCeof, exheight, exwidth);//调整数据
delete[] tempAlie;
tempAlie = NULL;
delete[] tempexlie;
tempexlie = NULL;
delete[] tempAhang;
tempAhang = NULL;
delete[] tempExhang;
tempExhang = NULL;
delete[] tempImage;
tempImage = NULL;
}
2)二维信号的单次重构
说明:
//二维小波反变换
void CWavelet::IDWT2(
double *pSrcCeof, //二维源图像系数数据
int dstHeight,//重构出来后数据的高度
int dstWidth,//重构出来后数据的宽度
double *pDstImage//重构出来的图像
)
{
int srcHeight = (dstHeight + m_dbFilter.filterLen - 1) / 2 * 2;
int srcWidth = (dstWidth + m_dbFilter.filterLen - 1) / 2 * 2;//pSrcCeof的高度
IAdjustData(pSrcCeof, srcHeight, srcWidth);//调整成LL,HL,LH,HH
double *tempAline = new double[srcHeight]; // 临时存放每一列的数据
double *tempdstline = new double[dstHeight]; // 临时存放每一列的重构结果
double *pTmpImage = new double[srcWidth*dstHeight];
// 列重构
for (int i = 0; i < srcWidth; i++)//每一列
{
// 列转置
for (int j = 0; j<srcHeight; j++)
tempAline[j] = pSrcCeof[j*srcWidth + i];//提取每一列
IDWT(tempAline, dstHeight, tempdstline);
// 反转置
for (int j = 0; j < dstHeight; j++)
pTmpImage[j*srcWidth + i] = tempdstline[j];
}
// 对每一行进行行变换
double *tempAhang = new double[srcWidth];
double *tempdsthang = new double[dstWidth]; // 临时存放每一行的处理数据
for (int i = 0; i < dstHeight; i++)
{
for (int j = 0; j < srcWidth; j++)
tempAhang[j] = pTmpImage[i*srcWidth + j];//提取每一行的数据
IDWT(tempAhang, dstWidth, tempdsthang);
for (int j = 0; j < dstWidth; j++)
pDstImage[i*dstWidth + j] = tempdsthang[j];
}
delete[] tempAline;
tempAline = NULL;
delete[] tempdstline;
tempdstline = NULL;
delete[] tempAhang;
tempAhang = NULL;
delete[] tempdsthang;
tempdsthang = NULL;
delete[] pTmpImage;
pTmpImage = NULL;
}
3)二维信号的多级分解
说明:对于每一级分解都将调用单次二维分解函数来实现,所以本函数是建立在函数IDW2基础上
// 二维小波多级分解,需要先初始化获取未来数据信息
bool CWavelet::WaveDec2(
double *pSrcData,//源图像数据,存储为一维信号
double *pDstCeof//分解后的系数,它的大小必须是m_msgCL2D.allSize
)
{
if (!m_bInitFlag2D)
{
cerr << "错误信息:未初始化,无法对图像进行分解!" << endl;
return false;
}
if (pSrcData == NULL || pDstCeof == NULL)//错误:无内存
return false;
int height = m_msgCL2D.msgHeight[0];
int width = m_msgCL2D.msgWidth[0];
int scale = m_msgCL2D.Scale;
// 临时变量,图像数据
double *tempImage = new double[height*width];
int maxCoefSize =4 * m_msgCL2D.msgHeight[1] * m_msgCL2D.msgWidth[1];
double *tempDst = new double[maxCoefSize];
for (int i = 0; i < height*width; i++)
tempImage[i] = pSrcData[i];
int gap = m_msgCL2D.allSize - maxCoefSize;
for (int i = 1; i <= scale; i++)
{
DWT2(tempImage, height, width, tempDst);
// 低频子图像的高和宽
height = m_msgCL2D.msgHeight[i];
width = m_msgCL2D.msgWidth[i];
for (int j = 0; j < height*width; j++)
tempImage[j] = tempDst[j];//提取低频系数(近似系数)
//
for (int j = 0, k = gap; j < 4 * height*width; j++, k++)
pDstCeof[k] = tempDst[j];//所有系数
gap -= 4 * m_msgCL2D.msgWidth[i + 1] * m_msgCL2D.msgHeight[i + 1] - height*width;
}
delete[] tempDst;
tempDst = NULL;
delete[] tempImage;
tempImage = NULL;
return true;
}
4)多级分解系数的重构
// 根据多级分解系数重构出二维信号,必须先初始化获取分解信息
bool CWavelet::WaveRec2(
double *pSrcCoef,//多级分解出的源系数
double *pDstData//重构出来的信号
)
{
if (!m_bInitFlag2D)
{
cerr << "错误信息:未初始化,无法对信号进行分解!" << endl;
return false;
}
if (pSrcCoef == NULL || pDstData == NULL)//错误:无内存
return false;
int height = m_msgCL2D.msgHeight[0];
int width = m_msgCL2D.msgWidth[0];
int decLevel = m_msgCL2D.Scale;
int maxCeofSize = 4 * m_msgCL2D.msgHeight[1] * m_msgCL2D.msgWidth[1];
double *pTmpImage = new double[maxCeofSize];
int minCeofSize = 4 * m_msgCL2D.msgHeight[decLevel] * m_msgCL2D.msgWidth[decLevel];
for (int i = 0; i < minCeofSize; i++)
pTmpImage[i] = pSrcCoef[i];
int gap = minCeofSize;
for (int i = decLevel; i >= 1; i--)
{
int nextheight = m_msgCL2D.msgHeight[i - 1];//重构出来的高度
int nextwidth = m_msgCL2D.msgWidth[i - 1];//重构出来的宽度
IDWT2(pTmpImage, nextheight, nextwidth, pDstData);
if (i > 1)//i==1已经重构出来了,不再需要提取系数
{
for (int j = 0; j < nextheight*nextwidth; j++)
pTmpImage[j] = pDstData[j];
for (int j = 0; j < 3 * nextheight*nextwidth; j++)
pTmpImage[nextheight*nextwidth + j] = pSrcCoef[gap + j];
gap += 3 * nextheight*nextwidth;
}
}
delete[] pTmpImage;
pTmpImage = NULL;
return true;
}
3,函数正确性验证
1)二维单次分解与重构测试
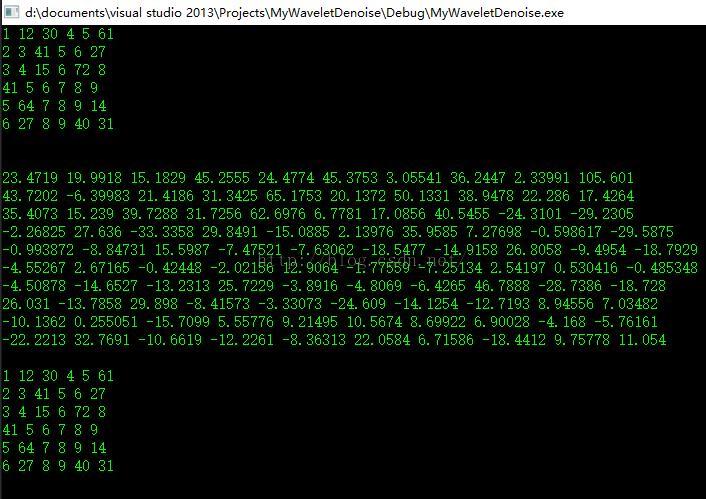
附带本次测试代码:
//小波函数的二维分解与重构
int main()
{
system("color 0A");
CWavelet cw;
double s[36] = { 1, 12, 30, 4, 5, 61, 2, 3, 41, 5, 6, 27, 3, 4, 15, 6, 72, 8, 41, 5, 6, 7, 8, 9, 5, 64, 7, 8, 9, 14, 6, 27, 8, 9, 40, 31 };
int height = 6;
int width = 6;
for (int j = 0; j < 36; j++)
{
cout << s[j] << " ";
if ((j + 1) % 6 == 0)
cout << endl;
}
cout << endl;
cout << endl;
cw.InitDecInfo2D(height, width, 1, 3);
double *dst = new double[cw.m_msgCL2D.allSize];
cw.DWT2(s, height, width, dst);
for (int j = 0; j < cw.m_msgCL2D.allSize; j++)
{
cout << dst[j] << " ";
if ((j + 1) % 10 == 0)
cout << endl;
}
cout << endl;
double *dsts = new double[36];
cw.IDWT2(dst, height, width, dsts);
for (int j = 0; j < 36; j++)
{
cout << dsts[j] << " ";
if ((j + 1) % 6 == 0)
cout << endl;
}
delete[] dst;
dst = NULL;
delete[] dsts;
dsts = NULL;
system("pasue");
return 0;
}
2)二维多级分解与重构测试
说明:对二维数据进行了5层分解,选取的是小波族db3

附带本次测试代码:
//小波函数二维多级分解与重构测试
int main()
{
system("color 0A");
CWavelet cw;
double s[48] = { 1, 12, 30, 4, 5, 61, 2, 3, 41, 5, 6, 27, 3, 4, 15, 6, 72, 8, 41, 5, 6, 7, 8, 9, 5, 64, 7, 8, 9, 14, 6, 27, 8, 9, 40, 31 ,
1, 12, 30, 4, 5, 61, 2, 3, 41, 5, 6, 27
};
int height = 6;
int width = 8;
for (int j = 0; j < 48; j++)
{
cout << s[j] << " ";
if ((j + 1) % 8 == 0)
cout << endl;
}
cout << endl;
int Scale = 5;
int dbn = 2;
cw.InitDecInfo2D(height, width, Scale, dbn);
double *dstcoef = new double[cw.m_msgCL2D.allSize];
cw.WaveDec2(s,dstcoef);
for (int i = 0; i < cw.m_msgCL2D.allSize; i++)
{
cout << dstcoef[i] << " ";
if ((i + 1) % 10 == 0)
cout << endl;
}
double *dst = new double[48];
for (int i = 0; i < 48; i++)
dst[i] = 0.0;
cw.WaveRec2(dstcoef, dst);
cout << endl; cout << endl;
for (int i = 0; i < 48; i++)
{
cout << dst[i] << " ";
if ((i + 1) % 8 == 0)
cout << endl;
}
cout << endl;
delete[] dst;
dst = NULL;
delete[] dstcoef;
dstcoef = NULL;
system("pause");
return 0;
}
3,阈值去噪结果:
说明:本测试只是模拟测试,对图像的处理也是一样的(完全一致)
硬阈值去噪结果
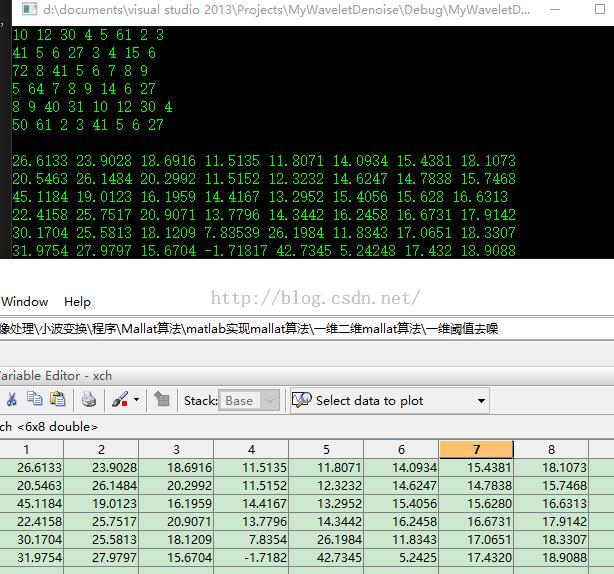
软阈值去噪结果
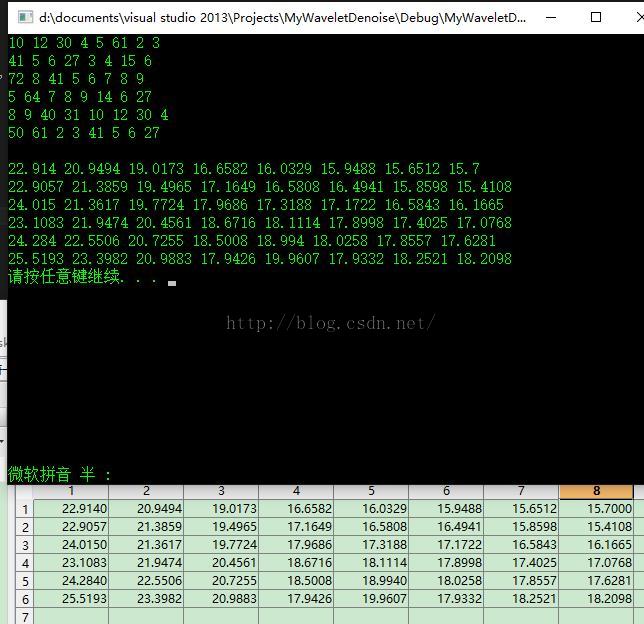
实际的图像处理结果为:
源噪声图像为:
注意以下是采用:db6,3层分解,软阈值去噪,阈值是在前文提及的阈值基础上缩小2.5倍得到的效果:
注意以下是采用:db6,3层分解,硬阈值去噪,阈值是在前文提及的阈值基础上缩小2.5倍得到的效果:
附带上述C++测试验证主函数
//二维阈值去噪测试
int main()
{
system("color 0A");
CWavelet cw;
double s[48] = { 10, 12, 30, 4, 5, 61, 2, 3, 41, 5, 6, 27, 3, 4, 15, 6, 72, 8, 41, 5, 6, 7, 8, 9, 5, 64, 7, 8, 9, 14, 6, 27, 8, 9, 40, 31,
10, 12, 30, 4, 50, 61, 2, 3, 41, 5, 6, 27};
int height = 6;
int width = 8;
for (int j = 0; j < 48; j++)
{
cout << s[j] << " ";
if ((j + 1) % 8 == 0)
cout << endl;
}
cout << endl;
int Scale = 3;
int dbn = 3;
cw.InitDecInfo2D(height, width, Scale, dbn);
double *dstcoef = new double[48];
if (!cw.thrDenoise2D(s, dstcoef))
cerr << "Error" << endl;
for (int j = 0; j < 48; j++)
{
cout << dstcoef[j] << " ";
if ((j + 1) % 8 == 0)
cout << endl;
}
delete[] dstcoef;
dstcoef = NULL;
system("pause");
return 0;
}
附带上述matlab验证程序
clc;
clear all;
close all;
% %%%%%%%%%%%%%%%%%%%%%%%%通过matlab的函数来实现阈值去噪%%%%%%%%%%%%%%%%%%%%%%%%%% %
X=[ 10, 12, 30, 4, 5, 61, 2, 3;
41, 5, 6, 27, 3, 4, 15, 6;
72, 8, 41, 5, 6, 7, 8, 9;
5, 64, 7, 8, 9, 14, 6, 27;
8, 9, 40, 31,10, 12, 30, 4;
50, 61, 2, 3, 41, 5, 6, 27];
X=double(X);
% 获取输入参数
wname = "db3";%小波类型
n = 3;%分解层数
sorh1 = "h";%硬阈值
sorh2 = "s";%软阈值
% 对图像进行小波分解
[c,l] = wavedec2(X,n,wname);
%求取阈值
N = numel(X);
[chd1,cvd1,cdd1] = detcoef2("all",c,l,1);
cvd1=cvd1(:)";
sigma = median(abs(cvd1))/0.6745;%提取细节系数求中值并除以0.6745
thr = sigma*sqrt(2*log(N));
% 对小波系数全局阈值处理
cxch = c;% 保留近似系数
cxcs = c;% 保留近似系数
justdet = prod(l(1,:))+1:length(c);%截取细节系数(不处理近似系数)
% 阈值处理细节系数
cxch(justdet) = wthresh(cxch(justdet),sorh1,thr);%硬阈值去噪
cxcs(justdet) = wthresh(cxcs(justdet),sorh2,thr);%软阈值去噪
%小波重建
xch = waverec2(cxch,l,wname);
xcs = waverec2(cxcs,l,wname);
注:本博文为EbowTang原创,后续可能继续更新本文。如果转载,请务必复制本条信息!
原文地址:http://blog.csdn.net/ebowtang/article/details/40481539
原作者博客:http://blog.csdn.net/ebowtang
参考资源:
【1】《数字图像处理》(冈萨雷斯matlab第二版)
【2】http://ivm.sjtu.edu.cn/files/wavelet/第3章wavelet_original.pdf
【3】http://media.cs.tsinghua.edu.cn/~ahz/digitalimageprocess/chapter12/chapt12_ahz.htm#a1
【4】http://wenku.baidu.com/link?url=OYRL2n-cYkZ2J10zaMscZQ-lhR05kysQ_CaB1YM1e_aqr3DakexZRm8rtBYOHlDmxC0cNAtiCopjyog_yOIH1zliUmyz2fKfOzFTAQ1wWj3
【5】《维基百科》
【6】来自中国知网若干论文
【7】小波分析及其应用__孙延奎
【8】杨建国.小波分析及其工程应用[M].北京:机械工业出版社.2005
【9】毛艳辉.小波去噪在语音识别预处理中的应用.上海交通大学硕士学位论文.2010
【10】matlab各种函数说明,及其内部函数实现