Unique Paths II

一. 题目描述

Follow up for “Unique Paths” : 
Now consider if some obstacles are added to the grids. How many unique paths would there be? 
An obstacle and empty space is marked as 1 and 0 respectively in the grid. 
For example, 
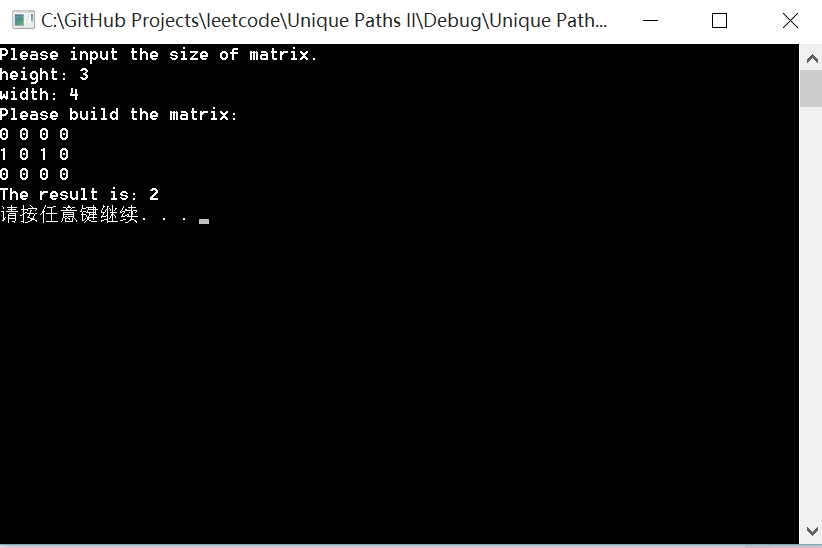
There is one obstacle in the middle of a 3 3 grid as illustrated below.

[
[0,0,0],
[0,1,0],
[0,0,0]
]

The total number of unique paths is 2. 
Note: m and n will be at most 100.

二. 题目分析

与上一题Unique Paths类似，但要特别注意第一列的障碍。在上一题中，第一列全部是1，但是在这一题中不同的是，第一列如果某一行有障碍物，那么后面的行应该为0。

三. 示例代码

使用动态规划：

#include <iostream>
#include <vector>
using namespace std;

class Solution
{
public:
    int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid)
    {
        const size_t x = obstacleGrid.size();    // 行数
        const size_t y = obstacleGrid[0].size(); // 列数
        vector<vector<int> > k;

        for (int i = 0; i < x; ++i)
            k.push_back(vector<int>(y, 0));

        for (int i = 0; i < x; ++i)
        {
            if (obstacleGrid[i][0] == 0) 
                k[i][0] = 1;
            else
            {
                for (int p = i; p < x; ++p)
                    k[p][0] = 0;
                break;
            }
        }

        for (int j = 0; j < y; ++j)
        {
            if (obstacleGrid[0][j] == 0)
                k[0][j] = 1;
            else
            {
                for (int q = j; q < y; ++q)
                    k[0][q] = 0;
                break;
            }
        }

        for (int i = 1; i < x; ++i)
        {
            for (int j = 1; j < y; ++j)
            {
                if (obstacleGrid[i][j] != 0) 
                    k[i][j] = 0;
                else
                    k[i][j] = k[i - 1][j] + k[i][j - 1];
            }
        }
        return k[x - 1][y - 1];
    }
};

四. 小结