дёҖ. йўҳзӣ®жҸҸиҝ°
Given s1; s2; s3, find whether s3 is formed by the interleaving of s1 and s2.В
For example, Given: s1 = вҖңaabccвҖқ, s2 = вҖңdbbcaвҖқ,В
When s3 = вҖңaadbbcbcacвҖқ, return true.В
When s3 = вҖңaadbbbacccвҖқ, return false.
дәҢ. йўҳзӣ®еҲҶжһҗ
жӯӨйўҳеҸҜдҪҝз”ЁдәҢз»ҙеҠЁжҖҒ规еҲ’жқҘи§ЈеҶіпјҢдёӢиЎЁз»ҷеҮәдәҶзӣҙи§Ӯзҡ„еҢ№й…ҚиҝҮзЁӢпјҡ
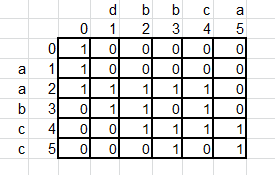
и®ҫжҹҗдёҖж јзҡ„зҠ¶жҖҒдёәk[i][j]пјҢиЎЁзӨәs1[i]жҲ–s2[j]пјҢдёҺs3[i+j]зҡ„еҢ№й…Қз»“жһңгҖӮs3еҸҜдёҺs1е’Ңs2зӣёеҢ№й…Қж—¶пјҢеҸҜеҲҶдёәд»ҘдёӢдёӨз§Қжғ…еҶөпјҡ
еҰӮжһңs1В зҡ„жңҖеҗҺдёҖдёӘеӯ—з¬ҰзӯүдәҺs3В зҡ„жңҖеҗҺдёҖдёӘеӯ—з¬ҰпјҢеҲҷk[i][j]=k[i-1][j]пјӣВ
еҰӮжһңs2В зҡ„жңҖеҗҺдёҖдёӘеӯ—з¬ҰзӯүдәҺs3В зҡ„жңҖеҗҺдёҖдёӘеӯ—з¬ҰпјҢеҲҷk[i][j]=k[i][j-1]гҖӮ
еӣ жӯӨзҠ¶жҖҒиҪ¬з§»ж–№зЁӢеҰӮдёӢпјҡВ f[i][j] = (s1[i - 1] == s3 [i + j - 1] && f[i - 1][j]) || (s2[j - 1] == s3 [i + j - 1] && f[i][j - 1]);
дёү. зӨәдҫӢд»Јз Ғ
#include <iostream>
#include <string>
#include <vector>
using namespace std;
class Solution
{
public:
bool isInterleave(string s1, string s2, string s3)
{
if (s3.size() != s1.size() + s2.size())
return false;
if (s3[0] != s1[0] && s3[0] != s2[0])
return false;
vector<vector<bool> > k(s1.size() + 1, vector<bool>(s2.size() + 1, false));
k[0][0] = true;
// иҫ№з•Ңи®ҫзҪ®
for (size_t i = 1; i <= s1.size(); ++i)
k[i][0] = (s1[i - 1] == s3[i - 1]) && k[i - 1][0];
for (size_t j = 1; j <= s2.size(); ++j)
k[0][j] = (s2[j - 1] == s3[j - 1]) && k[0][j - 1];
for (size_t i = 1; i <= s1.size(); ++i)
{
for (size_t j = 1; j <= s2.size(); ++j)
{
k[i][j] = ((s1[i - 1] == s3[i + j - 1]) && k[i - 1][j]) ||
((s2[j - 1] == s3[i + j - 1]) && k[i][j - 1]);
}
}
return k[s1.size()][s2.size()];
}
};
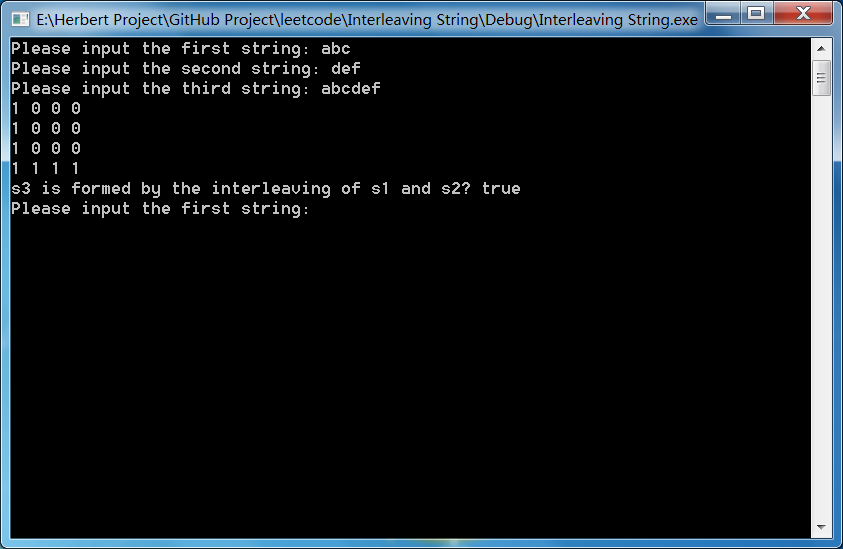
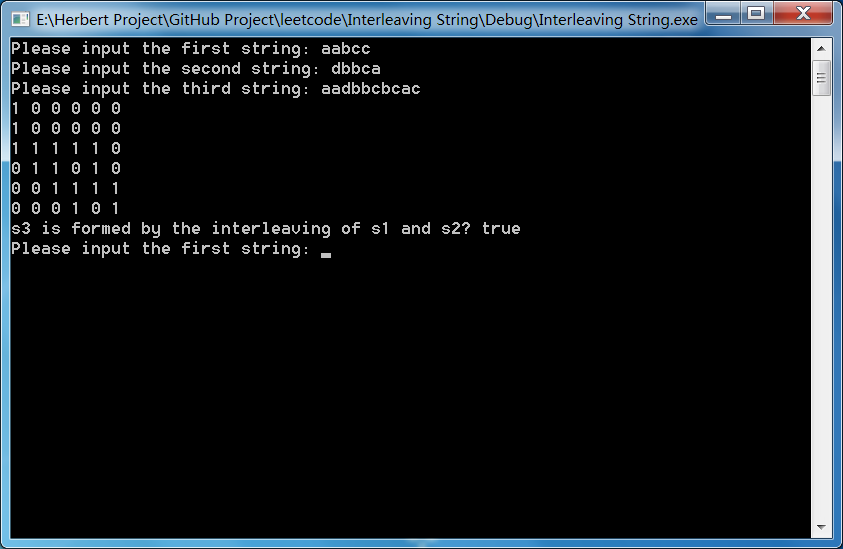
еӣӣ. е°Ҹз»“
зј–зЁӢж—¶иҰҒжіЁж„Ҹиҫ№з•ҢжқЎд»¶зҡ„й—®йўҳе’Ңж•°з»„зҡ„дёӢж Үй—®йўҳгҖӮ